Effect of Pore Space Stagnant Zones on Interphase Mass Transfer in Porous Media, for Two-Phase Flow Conditions

Abstract

Interphase mass transfer is an important solute transport process in two-phase flow in porous media. During two-phase flow, hydrodynamically stagnant and flowing zones are formed, with the stagnant ones being adjacent to the interfaces through which the interphase mass transfer happens. Due to the existence of these stagnant zones in the vicinity of the interface, the mass transfer coefficient decreases to a certain extent. There seems to be a phenomenological correlation between the mass transfer coefficient and the extent of the stagnant zone which, however, is not yet fully understood. In this study, the phase-field method-based continuous species transfer model is applied to simulate the interphase mass transfer of a dissolved species from the immobile, residual, non-aqueous phase liquid (NAPL) to the flowing aqueous phase. Both scenarios, this of a simple cavity and this of a porous medium, are investigated. The effects of flow rates on the mass transfer coefficient are significantly reduced when the stagnant zone and the diffusion length are larger. It is found that the stagnant zone saturation can be a proxy of the overall diffusion length of the terminal menisci in the porous medium system. The early-stage mass transfer coefficient continuously decreases due to the depletion of the solute in the small NAPL clusters that are in direct contact with the flowing water. The long-term mass transfer mainly happens on the interfaces associated with large NAPL clusters with larger diffusion lengths, and the mass transfer coefficient is mainly determined by the stagnant zone saturation.

Article highlights

• Flow rates can hardly affect the mass transfer coefficient when the stagnant zone and the diffusion length are large.

• The stagnant zone saturation can be a proxy of the overall diffusion length of the menisci in the porous media system.

• The correlations between the mass transfer coefficient and the stagnant zone saturations are built, based on simulations at different flow rates.

1 Introduction

Interphase mass transfer in porous media two-phase flow systems is an important process relevant in a wide range of scientific and engineering applications including the remediation of aquifers contaminated by non-aqueous phase liquids (NAPL) (Brusseau, 1992; Miller et al., 1990), geological storage of carbon dioxide (Schaffer et al., 2013; Tatomir et al., 2016), enhanced oil recovery (Graveleau et al., 2017), etc. In some of these applications, the dissolved chemical species (solute) in one phase of fluid may cross the interface and enter the other phase. The interphase mass transfer can be classified into different conditions depending on the fluid phase as the source of the species is mobile or immobile, wetting or non-wetting, according to Agaoglu et al. (2015). This study focuses on the interphase mass transfer process of the dissolved species from the residual immobile wetting liquid into the mobile non-wetting liquid in porous media.

1.1 Interphase Mass Transfer

The interphase mass transfer in porous media has been investigated both at the pore scale and at the macro-scale. At the pore scale, the pore structures and fluid–fluid interfaces are explicitly described in the studies. The interphase mass transfer occurs when the compound of interest has two individual chemical potentials with respect to each phase on both sides of the interface, and the thermodynamic equilibrium is violated (Weber et al., 1991). The upscaling techniques (e.g., volume averaging) have been widely used to derive the macro-scale equations from the pore-scale physics (Coutelieris et al., 2006; Kechagia et al., 2002; Quintard and Whitaker, 1994; Soulaine et al., 2011). Physical parameters are averaged over the representative element volume (REV) in the macro-scale studies. At the macro-scale, a common approach to determine the interphase mass transfer rate is to define it as the product of a mass transfer coefficient that is unique for the system, the interfacial area, and the driving force, which is determined by the difference between the current solute concentration in the solvent phase and the solute concentration in the solvent phase at thermodynamic equilibrium (Agaoglu et al., 2015; Miller et al., 1990). Thus, the interphase mass transfer rate can be formulated as:

$$\frac{dM}{dt}={k}_{f}{A}_{wn}({c}_{s}-c)$$

(1)

where M (kg) is interphase transferred solute mass, t (s) is time, A_wn (m²) is the interfacial area, c (kg/m³) is the current solute concentration, c_s (kg/m³) is the equilibrium solute concentration, and k_f (m/s) is the mass transfer coefficient. The mass transfer coefficient can be expressed in a dimensionless form as the Sherwood number:

$$Sh=\frac{{k}_{f}{L}_{c}}{D}$$

(2)

where L_c (m) is characteristic length equal to the mean grain diameter, and D (m²/s) is the solute molecular diffusion coefficient. In some studies, the interfacial area is not available, and thus a lumped mass transfer coefficient is introduced, which incorporates the above mass transfer coefficient k_f and the interfacial area (Brusseau, 1992; Imhoff et al., 1994; Miller et al., 1990). Since the interfacial area can be directly measured/estimated with pore-scale numerical simulation approaches, this study mostly focuses on the explicitly formulated mass transfer coefficient rather than the lumped mass transfer coefficient.

The mass transfer coefficient for a given system will approach a constant value after a certain period of time, due to the establishment of equilibrium in the driving forces and mass transfer rates (Miller et al., 1990; Soulaine et al., 2011). This mass transfer coefficient can be affected by many factors in the two-phase flow process, including interfacial area, saturation, flow rates, phase entrapments, NAPL distribution, NAPL mobilization, fluid density and viscosity, the physical properties of the porous medium, e.g., wettability, mean grain diameter, pore size distribution (Agaoglu et al., 2015), and the chemical properties of the NAPL and dissolved solute (Essaid et al., 2015). Flow velocity is considered an important parameter for interphase mass transfer since it determines the renewal of the compound near the interface (Graveleau et al., 2017). Numerous researches have been reported to build the correlations between the flow velocity (expressed as the Reynolds number or the Péclet number) and the mass transfer coefficient (expressed as the Sherwood number) (Aydin Sarikurt et al., 2017; Imhoff et al., 1994; Kennedy and Lennox, 1997; Miller et al., 1990; Powers et al., 1994b, 1994a, 1992). The proposed correlations are different depending on the properties of the porous material, the fluid saturations, the type of the NAPL, etc.

1.2 Effects of Stagnant Zones

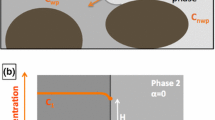
The stagnant zones are commonly defined as the regions with a very low flow velocity, casting diffusive mass transport (Karadimitriou et al., 2016). The non-wetting phase belonging to the stagnant zones and the flowing zones, and the residual wetting phase are distinguished in Fig. 1. It was found that the presence of stagnant zones can influence the tracer transport in unsaturated systems in the column experiments, i.e., larger longitudinal dispersion, early breakthrough and long tailings (Bond and Wierenga, 1990; Smedt and Wierenga, 1984; van Genuchten and Wierenga, 1976). The recent pore-scale micro-model experiments and numerical simulations further elaborate the critical roles the stagnant zones play in solute transport for two-phase fluids systems, e.g., affecting the dispersion coefficient, in correlation to the saturation topology and the relative permeability, etc. (Aziz et al., 2018; Dou et al., 2022; Hasan et al., 2020, 2019; Karadimitriou et al., 2017, 2016).

Fig. 1

Sketch of the distribution of the two phases of fluids involved in the solute interphase mass transfer in the porous media (black arrows show the flow direction), where flowing zones and stagnant zones of the non-wetting fluid are distinguished with the frame of solid lines and dashed lines

Besides, the existence of the stagnant zones is also an important factor affecting the interphase mass transfer rate and the mass transfer coefficient. With the use of pore-scale numerical simulation with the lattice Boltzmann method, Knutson et al. (2001) found that the interphase mass transfer is limited by the diffusive transport process through a thin zone of stagnant water at NAPL/water interface. Zhang et al. (2002) used magnetic resonance imaging to study NAPL dissolution in water-saturated flowthrough columns packed with angular silica gel of two different sizes. They found that the mass transfer coefficient was smaller in experiments with finer grains. This was attributed to the fact that finer grains led to the formation of a larger number of NAPL ganglia and an increment of the quantity of stagnant water adjacent to the interfaces. Thus, the extent of flowing water bypass (without contact to the interface) was increased in their system. These results are in agreement with the micromodel, fluorescence microscopy observations of Chomsurin and Werth (2003). They also found that the Sherwood number is highly dependent on the average diffusion length scale associated with the stagnant zones. Aminnaji et al., (2019) presented a pore-network model to study the NAPL dissolution, where links between the number of stagnant throats for different networks and the corresponding mass transfer coefficients are studied. They concluded that the NAPL mass transfer coefficient mainly depends on the distribution of the NAPL, rather than the interfacial area or the number of stagnant throats.

Despite the important findings in the above research studies, they were mostly focused on NAPL dissolution problems, where the species of interest is the NAPL itself rather than another species dissolved in it. One difference between these two conditions is the equilibrium solute concentration (c_s) in Eq. (1). For NAPL dissolution, the equilibrium concentration (c_s) is a constant equal to the solubility limit, while for interphase transfer of a dilute species (other than NAPL itself) the equilibrium concentration (c_s) is a variable dependent on its concentration in the NAPL. Thus, the mass transfer coefficients obtained from these two conditions can be different. To the authors’ knowledge, the effects of stagnant zones on the interphase transfer of dilute species in porous media were not yet studied. Furthermore, the stagnant zone is not directly quantified in these studies, e.g., by a stagnant zone saturation (the ratio of the volume of the stagnant zone to the total volume of pore space). Thus, the parameters representing the extent of the stagnant zones (e.g., stagnant zone saturation) have not yet been used to build the correlations for the characterization of interphase mass transfer. It is worth noting that the effects of stagnant zones cannot be represented with the fluid saturation in the correlations, because it has been shown that the volume of the stagnant zone depends in a non-monotonic way on the saturation for a fixed saturation topology (Dou et al., 2022; Hasan et al., 2020; Karadimitriou et al., 2017, 2016). How the mass transfer coefficients change with respect to different volumes of the stagnant zone at different saturations is not fully understood. Therefore, the correlation between the stagnant zone saturation and the mass transfer coefficient will be studied here by performing a pore-scale investigation using direct numerical simulation.

1.3 Numerical Methods at Pore Scale

The pore-scale numerical simulations of the interphase mass transfer have been done with the pore network models (PNM) (Dillard et al., 2001; Dillard and Blunt, 2000; Held and Celia, 2001; Jia et al., 1999; Zhao and Ioannidis, 2003). However, the previous studies using PNM are mostly regarding to the NAPL dissolution, and the simplified representations of the pore space may make the calculation of the stagnant zones saturation inaccurate. As an alternative, computational fluid dynamics (CFD) approaches can be used for simulation of the interphase mass transfer in complex (natural) pore structures. The CFD approaches, e.g., the volume-of-fluid method (VOF), the level-set method (LSM), the phase-field method (PFM), solve the Navier–Stokes equations in a discretized domain, and the interface between the two fluids is represented by an indicator function (Graveleau et al., 2017; Maes and Soulaine, 2018). One major challenge for the simulation of species interphase mass transfer with the CFD method is the handling of the concentration jump at the fluid–fluid interface (Graveleau et al., 2017). This problem is solved by Haroun et al., (2010a) with a new single-field Continuous Species Transfer (CST) formulation. The CST formulation, developed in the framework of the VOF method, introduced a constant partitioning coefficient in the transport equation to describe the thermodynamic equilibrium of the species at the fluid–fluid interface (Haroun et al., 2010a). The VOF-CST model was successfully applied to simulate the interphase mass transfer in liquid film flow along corrugated surfaces (Haroun et al., 2012, 2010b), in bubble flow (Deising et al., 2016; Marschall et al., 2012), and in subsurface two-phase flow problems with moving contact lines (Graveleau et al., 2017). Yang et al. (2017) found that the solute mass partitioning between two phases is not accurately simulated by the VOF-CST model at high Péclet numbers, due to the numerical diffusion in the phase concentration. By adding a compressive term in the transport equation, Maes and Soulaine (2018) managed to improve the VOF-CST model by significantly diminishing the numerical errors. Gao et al. (2021a) further derived the CST formulations based on the PFM, and the model was labelled as PFM-CST. Both approaches have their pro and con. The PFM with a smooth indicator function can better simulate the curvature and smooth physical quantities at the interface (Akhlaghi Amiri and Hamouda, 2013). However, the PFM is generally more computationally expensive due to the necessity to resolve the diffusive interface on a fine grid (Maes and Soulaine, 2018).

1.4 Objectives

In this study, we employ the previously developed PFM-CST models to simulate the interphase mass transfer of a dissolved dilute species in the residual immobile NAPL, into the flowing water, in a cavity and in a porous medium. We focus on the understanding of how the stagnant zones affect the mass transfer coefficient at the pore scale. The novelty of the paper is that the correlations between the mass transfer coefficient (for interphase transfer of dilute species) and the parameters representing the extent of the stagnant zones (the stagnant zone saturation and the average diffusion length) are first time investigated, at different water flow rates and different saturation topologies. For the porous medium domain, different phase distribution patterns (with different volumes of stagnant zones) are obtained from the displacement processes at different flow rates in the preparatory step.

The paper is organized as follows: Sect. 2 reviews the mathematical model. In Sect. 3, we explain the numerical implementation and the details of the numerical setup and data processing. The simulation results and discussions are demonstrated in Sect. 4, and in Sect. 5, finally, we list the main conclusions.

2 Mathematical Model

2.1 Phase-Field Method

The basic theory of the PFM is first reviewed briefly here according to the studies, e.g., (Alpak et al., 2016; Basirat et al., 2017; Jacqmin, 1999; Yue et al., 2004). In the PFM, sharp interface between two fluid phases is replaced by a diffusive interfacial layer, with a small but finite thickness (Basirat et al., 2017). Following Yue et al. (2004), a phase variable ($\phi$), changing smoothly between -1 and 1, is introduced to describe the composition of the fluid mixture at the interface. Thus, the volume fractions of two fluids (V_f) are defined as $\frac{1-\phi }{2}$ and $\frac{1+\phi }{2}$, respectively. The $\phi$ profile across the interface is determined by the free energy density (Alpak et al., 2016). The free energy density (mixing energy) (J/m³) for isothermal mixing of two fluids can be expressed in the Ginzburg–Landau form (Yue et al., 2006):

$${f}_{\mathrm{mix}}\left(\phi ,\nabla \phi \right)=\frac{1}{2}\lambda {\left|\nabla \phi \right|}^{2}+\frac{\lambda }{4{\varepsilon }^{2}}{\left({\phi }^{2}-1\right)}^{2}$$

(3)

where λ (N) is the magnitude of the mixing energy and ε (m) is a capillary thickness which determines the thickness of the diffusive interface. The free energy density (in Eq. 3) is composed of the surface energy (the first term) and the bulk energy (the second term) (Basirat et al., 2017). The chemical potential G (J/m³) is calculated by the variation of the free energy with respect to $\phi$:

$$G=\frac{\updelta \underset{\Omega }{\overset{}{\int }}{f}_{\mathrm{mix}} dx}{\updelta \phi }=-\lambda {\nabla }^{2}\phi +\frac{\lambda }{{\varepsilon }^{2}}{\phi (\phi }^{2}-1)$$

(4)

where $\Omega$ is the spatial domain occupied by the two fluid phases. The interfacial tension, defined as the total free energy at the interface per unit area of the interface, is in relation to the capillary thickness and the magnitude of the mixing energy through (Jacqmin, 1999; Yue et al., 2004):

$$\sigma =\frac{2\sqrt{2}\lambda }{3\varepsilon }$$

(5)

Assuming that the diffusive fluid flux is proportional to the gradient of the chemical potential, fluid mass conservation can be described by the Cahn–Hilliard equation (Cahn and Hilliard, 1959):

$$\frac{\partial \phi }{\partial t}+\mathbf{u}\cdot \nabla \phi =\nabla \cdot (\gamma \nabla G)$$

(6)

where u is the fluid velocity vector and γ (m³s/kg) is the mobility. The mobility is necessary to be large enough to keep a constant interfacial thickness, but small enough not to suppress the flow (Jacqmin, 1999). The mobility can be formulated as a function of the capillary thickness and a tuning factor: $\gamma =\chi {\varepsilon }^{2}$ (Akhlaghi Amiri and Hamouda, 2013).

2.2 Two-Phase Flow Dynamics

Momentum conservation is governed by the incompressible form of the Navier–Stokes equation, where the surface tension force is considered as a body force according to Yue et al. (2006) $\left( { - \frac{{{\updelta }\mathop \smallint \nolimits_{\Omega }^{{}} f_{{{\text{mix}}}} dx}}{{{\updelta }{\varvec{x}}}} = G\nabla \phi } \right)$, and the gravity effects are neglected due to the horizontal setup in Sect. 3.2:

$$\rho \left( {\frac{{\partial {\mathbf{u}}}}{\partial t} + {\mathbf{u}} \cdot \nabla {\mathbf{u}}} \right) = \nabla \cdot \left[ { - p{\mathbf{I}} + \mu \left( {\nabla {\mathbf{u}} + \left( {\nabla {\mathbf{u}}} \right)^{T} } \right)} \right] + G\nabla \phi$$

(7)

$$\nabla \cdot \mathbf{u}=0$$

(8)

where u (m/s) is the fluid velocity vector, p (Pa) is pressure, I is the second-order identity tensor, μ (Pa·s) is the dynamic viscosity, and ρ (kg/m³) is the density. It is worth noting that the incompressible formalism of the Navier–Stokes equation can be applied for the fluid mixture at the interface as long as the interface thickness is adequately small and the results are unaffected (Gao et al. 2021b). Besides, it is assumed that the fluid properties are not affected by the solute transport, meaning ρ and μ are independent of the solute concentration. This is reasonable because the solute has small mass compared to the bulk fluid phases. μ and ρ are calculated as:

$$\rho = \rho_{w} V_{f,w} + \rho_{nw} V_{f,nw} \;{\text{and}}\;\mu = \mu_{w} V_{f,w} + \mu_{nw} V_{f,nw}$$

(9)

where V_f,w and V_f,nw indicate the volume fraction of the wetting fluid and the non-wetting fluid, respectively. A no-slip boundary is applied at the grain surfaces, which implies that u = 0 in the momentum equation for wall boundaries. The contact angle on the solid wall is defined as:

$$\mathbf{n}\cdot \nabla \phi =\mathrm{cos}{\theta }_{w}\left|\nabla \phi \right|$$

(10)

where n is the (outward) normal vector to the wall and ${\theta }_{w}$ is the contact angle. With the diffusive fluxes between the bulk fluids (Eq. 6), the contact line on the wall results effectively in slip (Gao et al., 2021a). Thus, additional settings about the contact line moving, which are necessary for VOF-CST models reported by Graveleau et al. (2017), are not required here.

2.3 Solute Transport

The continuous species transfer model, based on the phase-field method, is derived and explained in Gao et al. (2021a, 2021b). The species interphase mass transfer includes several major mechanisms, i.e., advection, molecular diffusion, and partitioning. The chemical species considered here is considered as solute in both of the fluid phases, which means the solubility limit is not exceeded and no precipitation occurs. In this section, we review in brief the equations implemented in the solute transport model. Firstly, for species k dissolving in fluid phase α with the mass concentration of ${c}_{a,k}$, the solute mass conservation equation writes (Gao et al., 2021a):

$$\left\{\begin{array}{c}\frac{\partial {{(V}_{f,w}c}_{w,k})}{\partial t}+\nabla \cdot (u{V}_{f,w}{c}_{w,k}+0.5\gamma \nabla G{c}_{w,k})=0\\ \frac{\partial {{(V}_{f,nw}c}_{nw,k})}{\partial t}+\nabla \cdot (u{V}_{f,nw}{c}_{nw,k}-0.5\gamma \nabla G{c}_{nw,k})=0\end{array}\right.$$

(11)

where the dominant transport process due to the bulk fluid motion (i.e., advection) is described in Eq. (11). The local thermodynamic equilibrium of the solute at the interface is described by a partitioning coefficient (P_ow,k), which is defined as the concentration ratio of the species in each phase, at equilibrium.

$${P}_{ow,k}=\frac{{c}_{nw,k}}{{c}_{w,k}}$$

(12)

where c_nw,k and c_w,k are the concentration of the solute in the non-wetting phase and the wetting phase, respectively. The single-field formulation of the species concentration for both phases in the entire domain is obtained by defining the global concentration (c_k) as:

$${c}_{k}={{V}_{f,w}c}_{w,k}+{{V}_{f,nw}c}_{nw,k}$$

(13)

Therefore, the sum of the mass conservation Eq. (11) for species k in both phases writes:

$$\frac{\partial {c}_{k}}{\partial t}+\nabla \cdot \left[\mathbf{u}{c}_{k}+0.5\gamma \nabla G\left({c}_{w,k}-{c}_{nw,k}\right)\right]=0$$

(14)

The mechanisms of molecular diffusion are considered by a diffusion term, where the molecular diffusion flux for the mixture is defined as in (Haroun et al., 2010a):

$${\mathbf{J}}_{k}={{{D}_{k}(V}_{f,w}\nabla c}_{w,k}+{{V}_{f,nw}\nabla c}_{nw,k})={D}_{k}[\nabla {c}_{k}-\left({c}_{w,k}{-c}_{nw,k}\right)\nabla {V}_{f,w}]$$

(15)

As V_f,w + V_f,nw = 1, here only V_f,w is used in the expression, and the molecular diffusion coefficient is expressed as:

$${D}_{k}=\frac{1}{\frac{{V}_{f,w}}{{D}_{w,k}}+\frac{{V}_{f,nw}}{{D}_{nw,k}}}$$

(16)

It is reported that the harmonic interpolation of the diffusion coefficient for the mixture is more robust than a simple mixing rule (Deising et al., 2016; Maes and Soulaine, 2020). The diffusion flux (Eq. 16) consists of two parts: one flux driven by the concentration gradient, and the other flux resulting from the solubility law, which is in the direction normal to the interface. This flux resulting from the solubility law governs the partitioning of the solute between the two phases (Gao et al., 2021a). With the definition of Eq. (13) and Eq. (14), one obtains:

$${c}_{w,k}{-c}_{nw,k}=\frac{{c}_{k}(1-{P}_{ow,k})}{{V}_{f,w}+{P}_{ow,k}(1-{V}_{f,w})}$$

(17)

The final governing equation for the global concentration of species k is obtained by incorporating Eq. (18) and Eq. (16) into Eq. (15):

$$\begin{gathered} \frac{{\partial c_{k} }}{\partial t} + \nabla \cdot \left[ {{\mathbf{u}}c_{k} + 0.5\gamma \nabla G\frac{{c_{k} \left( {1 - P_{ow,k} } \right)}}{{V_{f,w} + P_{ow.k} \left( {1 - V_{f,w} } \right)}}} \right] \hfill \\ - \nabla \cdot \left[ {D_{k} \left( {\nabla c_{k} - \nabla V_{f,w} \frac{{c_{k} \left( {1 - P_{ow,k} } \right)}}{{V_{f,w} + P_{ow,k} \left( {1 - V_{f,w} } \right)}}} \right)} \right] = 0 \hfill \\ \end{gathered}$$

(18)

3 Numerical Details

We explain the model implementation in Sect. 3.1, the setup of the model in Sect. 3.2, and the data treatment process in Sect. 3.3.

3.1 Numerical Implementation

The model is implemented in the software COMSOL Multiphysics™ (V5.5), using the basic module and the CFD module. COMSOL employs the finite element method for spatial discretization (Gao et al., 2021b). The linear solver PARDISO is used to solve the discretized partial differential equations, and the backward Euler method is used for calculating the time stepping. The initial time step and maximum time steps are automatically adjusted so that singularities are avoided (Akhlaghi Amiri and Hamouda, 2013). The mesh generator in COMSOL uses the advancing front algorithm to calculate the tessellation, and the mesh elements are in triangles (Gao et al., 2021b). The computer has a single CPU with 8 cores, operating at 4.3 GHz, and 128 GB RAM. The numerical implementation of the model in COMSOL has been verified in the previous study by comparing it with one-dimensional analytical solutions for several processes, including solute advective diffusion and transient interphase mass transfer processes (Gao et al., 2021a).

3.2 Model Setup

The effect of the stagnant zones on the interphase mass transfer is studied based on two scenarios: (1) a single cavity and (2) a porous medium. The domains for simulation in both scenarios are horizontal setups, and thus, the gravity is irrelevant. The properties of the fluids are considered to be the same in both scenarios: ρ_water = 1000 kg/m³, μ_water = 1 × 10^–3 Pa·s, ρ_NAPL = 840 kg/m³, and μ_NAPL = 6.5 × 10^–3 Pa·s. The water properties correspond to pure water at 20 °C, and the NAPL properties correspond to a North Sea crude oil (Mahani et al., 2014). The interfacial tension σ = 0.01 N/m, and the NAPL is assumed as the wetting phase with the contact angle of θ_w = 135° according to the simulation by Maes and Soulaine, (2018). The solute for simulation is a contaminant k, with the partitioning coefficient P_ow = 0.5, the initial concentration of 1 kg/m³, and the molecular diffusion coefficient D_k = 1 × 10^–9 m²/s (Maes and Soulaine, 2018). The contaminant k is initially dissolved in the NAPL, and it is being removed from the domain by mass transfer into the flowing water. The characteristic mobility, χ, is chosen between 10 and 100, so that the thickness and configuration of the interface is ensured to be invariant during the mass transfer process, according to Appendix 1. The capillary thickness (ε) and the mesh size (h) are chosen small enough to ascertain mesh convergence and model convergence (Gao et al., 2021a). On the other hand, the mesh size (h) cannot be too small to make the computational cost unaffordable.

3.2.1 Study of Interphase Mass Transfer in a Cavity

The interphase mass transfer process is first studied in a single cavity, with only one interface being involved. The intention of the numerical setup is to fix the interfacial area, initial solute concentration in NAPL and NAPL volume in all simulations, so that the changes in the mass transfer coefficient are mainly studied in relation to different sizes of the stagnant zones (space occupied by the immobile water) and different flow velocities. The setup of the cavity is illustrated in Fig. 2, where the top rectangular represents a flow channel and the bottom rectangular represents a throat with stagnant fluids. Water is injected at the left-hand boundary at inflow velocities of 1 × 10^–2 m/s, 1 × 10^–3 m/s, and 1 × 10^–4 m/s, with the right-hand boundary as the outlet with a constant pressure p = 0. The initial solute concentration in water and the concentration at inlet are both zero (left boundary with constant concentration c_k = 0). The right boundary (outlet) is defined as $\nabla \cdot ({D}_{k}\nabla {\mathrm{c}}_{k})$=0. NAPL is located at the bottom of the throat (measuring 0.1 mm × 0.1 mm), with initial solute concentration of 1 kg/m³. The region between the NAPL and the flowing channel is associated with the stagnant zone, with a length of L, as shown in Fig. 2. Simulations are carried out with the stagnant zones bearing three different lengths: L₁ = 0.03 mm, L₂ = 0.1 mm, and L₃ = 0.18 mm, at each inflow velocity. Thus, in total nine simulations are done for the study in the cavity. The characteristic length, in this case, is equal to the width of the throat L_c = 0.1 mm. The two-phase flow system is first simulated for a short period of 0.01 s, and the system reaches a steady state with the interface configuration matching the given contact angle. Then, the simulation of the solute transport and interphase mass transfer begins, and the results are recorded. The mesh size for the model is set at h = 2 × 10^–6 m, and the capillary thickness is ε = 2 × 10^–6 m. The characteristic mobility is chosen χ = 10. The simulation of interphase mass transfer is terminated after depletion of at least 80% of the initial mass of the species k, and a constant mass transfer coefficient for the system is ensured to be obtained. The domain in Fig. 2 is discretized by 16,088 elements. The time step is 0.1 s, and the total simulations time is 40 s. Due to the simple setup of the cavity, the runtime of each simulation lasts ca. 1 h.

Fig. 2

Plot of the geometry and boundary conditions of the cavity

3.2.2 Study of Interphase Mass Transfer in a Porous Medium

The solute interphase mass transfer is studied next in a two-dimensional porous medium, for several saturation topologies with different volume fractions of the stagnant zones. It is worth noting that compared to a three-dimensional medium, the major difference is, e.g., pore coordination number, the permeability of the porous medium, and the connectivity of the wetting phase, but physics in the processes remain comparable. The pore space is shaped by circular grains, which have been widely used in micro-model experiments and pore-scale numerical studies (Anna et al., 2014; Ferrari and Lunati, 2013; Godinez-Brizuela et al., 2017; Liu et al., 2014; Soulaine et al., 2021). The size of each grain is chosen randomly from diameters of 225 μm, 250 μm, or 275 μm. The grains are first uniformly distributed to fill the domain (Fig. 3b), followed by a random shift from its original place in both x- and y-directions. The distances of the random movements of the grains are controlled to be shorter than 20 μm, so that the grains do not overlap. The 2D geometry is generated at a porosity of 47.56%, measuring 7.36 mm × 3.53 mm in size, as shown in Fig. 3a. The triangular mesh elements have a side length of h = 6 × 10^–6 m, and two layers of mesh on the solid wall are further refined to 1.5 × 10^–6 m, as shown in Fig. 3c. The mesh consists of in total 1,249,369 elements. The capillary thickness for the model is set at ε = 7 × 10^–6 m.

Fig. 3

Plot of (a) the geometry and boundary conditions of the porous medium (pore space in dark gray color); (b) the initial uniform distribution of circle grains; and (c) finite element mesh generated with triangular elements

The simulation is carried out in two steps: a preparation step to simulate the two-phase flow and obtain a steady state saturation topology, and a main step to simulate the interphase mass transfer. In the preparation step, the main domain with the porous material is initially filled with the NAPL, and an extensive rectangular zone serving as an inlet on the left-hand side is initially filled with water. The extensive rectangular zone (measuring 0.12 mm × 3.53 mm in size) has the same width as the study domain and a small length to save the computational cost. The initial location of the interface is provided in the red dashed line in Fig. 3a, important to ascertain numerical stability. Water is injected at a constant specific flux of 0.1 m/s, 0.05 m/s, 0.04 m/s, and 0.02 m/s from the left boundary, to displace the NAPL. The characteristic mobility is chosen χ = 100, χ = 50, χ = 40 and χ = 20, respectively. The right-hand side of the domain is the outlet with a constant pressure p = 0, and the upper and lower sides of the domain are symmetry (free-slip and non-penetrating) boundaries. The simulations of displacement processes last until steady-state saturation topologies at the given flow rates are obtained. The time step is set at 0.002 s, and the total simulation time 1.2 s. The runtime ranges between 100 and 150 h for each simulation of two-phase flow (preparation step). Next, the main step for simulation of the mass transfer starts. At each of the four saturation topologies, three water inflow velocities of 1 × 10⁻² m/s, 1 × 10⁻³ m/s, and 1 × 10⁻⁴ m/s are simulated. Thus, in total 12 simulations are done in this study. The inflow velocities in the main step are smaller than those in the preparation step so that the saturation topologies remain unchanged (Karadimitriou et al., 2017). The initial solute concentration is 0 in water and 1 kg/m³ in NAPL. The left boundary is constant concentration c_k = 0, and the right boundary is defined as $\nabla \cdot \left({D}_{k}\nabla {\mathrm{c}}_{k}\right)$=0. The characteristic length, in this case, is equal to the averaged width of the throat in the porous media L_c = 0.062 mm (estimated from distances between centers of the circular grains). The simulation of interphase mass transfer is terminated after depletion of at least 95% of the initial mass of the species k. The time step is set as 1 s, and the total simulation time ranges between 100 and 500 s, depending on different degrees of saturation. The runtime is ca. 5 h for each simulation of the interphase mass transfer (main step).

3.3 Data Treatment

The macroscopic parameters of the system (average phase concentration, mass transfer rate, interfacial area) can be determined by post-processing the pore-scale simulation results. The average phase concentration of the dissolved solute k can be obtained as:

$${c}_{\mathrm{NAPL}}=\frac{{\int }_{{V}_{\mathrm{NAPL}}}{c}_{k}dV}{{\int }_{{V}_{\mathrm{NAPL}}}dV}\,\, \rm{ and} \,\,{c}_{\mathrm{water}}=\frac{{\int }_{{V}_{\mathrm{water}}}{c}_{k}dV}{{\int }_{{V}_{\mathrm{water}}}dV}$$

(19)

where V_NAPL is the region in the domain where V_f,w > 0.5 and V_water is the region in the domain where V_f,w < 0.5. Since the NAPL in the domain does not flow, the interphase mass transfer rate can be directly obtained by monitoring the changing rate of total solute mass in the NAPL. The total solute mass in the NAPL can be calculated as:

$${M}_{\mathrm{NAPL}}={\int }_{{V}_{\mathrm{NAPL}}}{c}_{k}dV$$

(20)

and then the interphase mass transfer rate at time step t_n can be obtained as:

$$dM/dt{|}_{{t}_{n}}=\frac{{M}_{\mathrm{NAPL}}{|}_{{t}_{n}}-{M}_{\mathrm{NAPL}}{|}_{{t}_{n+1}}}{\Delta t}$$

(21)

where $\Delta t$ is the time interval between t_n+1 and t_n. The diffusive interfacial area, as the region with ${V}_{f,w}\in \left[0.05, 0.95\right]$ according to Gao et al. (2021a), can be calculated with:

$${A}_{\mathrm{wn}}^{\mathrm{dif}}={\int }_{{V}_{\mathrm{interface}}}dV$$

(22)

where V_interface is the region in the domain with 0.05 < V_f,w < 0.95. The diffusive interfacial area (${A}_{\mathrm{wn}}^{\mathrm{dif}}$) can be converted into a sharp interfacial area (A_wn) and the corresponding specific interfacial area (a_wn) by:

$${A}_{\mathrm{wn}}=\frac{{A}_{\mathrm{wn}}^{\mathrm{dif}}}{{b}_{\mathrm{wn}}}\,\, \rm{and} \,\,{a}_{\mathrm{wn}}=\frac{{A}_{\mathrm{wn}}}{{V}_{\mathrm{pm}}}$$

(23)

where b_wn is the thickness of the diffusive interface, b_wn = 4.1641ε calculated with Eq. (4) at G = 0 according to Gao et al. (2021a), and V_pm is volume of the porous medium. The flowing and stagnant zones are distinguished by the threshold local Péclet number, defined in Sect. 4.

4 Results and Discussion

The results of the cavity study are shown in Sect. 4.1, and those investigating the porous medium set up in Sect. 4.2.

4.1 Interphase Mass Transfer in a Cavity

First, the simulated velocity profiles in the cavity at inflow velocity u_in = 1 × 10^–2 m/s at three stagnant zones lengths (L₁ = 0.03 mm, L₃ = 0.1 mm and L₅ = 0.18 mm) are shown as examples in Fig. 4a. The stagnant and flowing zones can be distinguished by a local threshold Péclet number. The local Péclet number is calculated as ${Pe}_{l}=\Vert \mathrm{u}\Vert *{L}_{c}/{D}_{k}$, where u is the flow velocity obtained from the simulation results, L_c is a characteristic length equal to the throat width, and D_k is the molecular diffusion coefficient. The local threshold Péclet number can be chosen by analyzing its probability distribution (Aziz et al., 2018). The probabilities are calculated as the ratio of the pore space at the given interval of local Péclet number (e.g., log₁₀(Pe_l)$\in [-0.1, 0]$, log₁₀(Pe_l)$\in [0, 0.1]$, etc.) to the total pore space. The probability distributions of the local Péclet number for the examples in Fig. 4c show multimodal distributions (Hasan et al., 2020). The first large peak observed at the right-hand side indicates the regions of flowing water, and the first small peak from the left-hand side indicates regions of the immobile NAPL, where flow velocity is about four orders of magnitude lower than that in the flowing zones. The small peaks in the middle (for L₂ and L₃ in Fig. 4c) indicate the stagnant zones, where weak recirculating flow exists with the velocity being about two orders of magnitude smaller than that in the flowing zones. The local threshold Péclet number is chosen as Pe_l = 10^–0.3 (indicated by red dashed line in Fig. 4c), to differentiating the flowing and stagnant water. The distinguished NAPL, stagnant water, and flowing water are plotted in Fig. 4b. There is almost no stagnant zone when the interface is close to the flowing region (see L₁ in Fig. 4b). The stagnant zone can be a recirculation zone of low velocity (see L₂ in Fig. 4b), or a combination of a fully stagnant zone and a recirculation zone with a large length (see L₃ in Fig. 4b).

Fig. 4

Simulation results of the velocity profiles in the cavity at inflow velocity u_in = 1 × 10^–2 m/s, with stagnant zone lengths of L₁, L₂, and L₃: (a) velocity distribution; (b) distinguished mobile and immobile zones with the NAPL indicated by grey color (the white arrows show the direction of the velocity vector, and the length of the arrows is proportional to the natural logarithm of the length of velocity vector); (c) probability distribution of the local Péclet number, with the interval of log₁₀(Pe_l) = 0.1

Then, the mass transfer processes at u_in = 1 × 10^–4 m/s at stagnant zones lengths of L₁ = 0.03 mm and L₅ = 0.18 mm are compared and shown as examples in Fig. 5. The average phase solute concentration in both NAPL and water is higher when the length of the stagnant zone (measured between the NAPL-water interface and the flow channel) is larger (Fig. 5a). This is because the larger length of the stagnant zone is, the longer the time of the overall mass transfer of the solute from NAPL into the moving water is, and thus the magnitude of solute mass being flushed by the moving water is lower. For convenience, we name the depth of path of diffusive solute transport in the stagnant water the diffusion length. The interphase mass transfer rate is plotted in Fig. 5b. At the beginning stage for the first 3 s, the mass transfer rates are large, as the solute is transferred from NAPL to the pure water. The mass transfer rates are close for the simulations of L₁ and L₃, and the mass transfer rates decrease fast. From 3 to 35 s, the mass transfer rate is significantly lower for larger stagnant zone. Because in stagnant water diffusion-dominated transport is much slower compared to advection-controlled transport in the flowing water, a higher solute concentrations develop in the stagnant water region (see Fig. 5c) compared to those in the regions of mobile water. Thus, the concentration gradient next to the interface, performing as the driving force, is decreased because of the presence of the stagnant zone. This leads to a lower interphase mass transfer rate. After 35 s, the interphase mass transfer rate of the simulations with stagnant zones (L₃) can be slightly larger compared to that without stagnant zones (L₁), due to lower solute mass remaining in L₁. The solute concentration distributions at t = 1 s, t = 3 s, and t = 8 s are plotted in Fig. 5c. The concentration is plotted in a logarithm so that the solute flux during mass transfer can be better resolved. It is observed that at t = 1 s, the simulation of L₃ is still at the stage of initial diffusive transport in the stagnant water, and for L₁ the solute flux is already approaching the region of flowing water because there is almost no stagnant zones. It is also observed that the recirculating flow can promote the solute transport in the stagnant zones (see Fig. 5c at t = 3 s) and affect the established solute concentration profile (see Fig. 5c at t = 8 s).

Fig. 5

Simulation results of the mass transfer processes at u_in = 1 × 10^–4 m/s at stagnant zones lengths of L₁ and L₅: (a) plot of the phase averaged concentration; (b) plot of the interphase mass transfer rate versus the time; and (c) plot of the solute concentration distribution at t = 1 s, t = 3 s, and t = 8 s

Furthermore, the macroscopic parameters, i.e., average phase concentration, mass transfer rates, and interfacial area, are obtained from simulation results as explained in Sect. 3.3. In Fig. 6a–c, mass transfer rates per (sharp) interfacial area are plotted against the driving force (concentration difference as a proxy) for all simulations. The slope of curves indicates the corresponding mass transfer coefficients, according to Eq. (1). The crosses in the figure show the times of the beginning of the simulations, the arrival of the constant slope of the data curves, and the end of the simulations. It can be observed that in all cases, the mass transfer coefficients (slopes of the corresponding curves) decrease for the transient mass transfer process at the beginning, and this is due to the rapid drop in the magnitude of the driving force at the beginning. A linear trend can be observed after a short period of time: about 2.4 s for L₁, 3.7 s for L₂, and 5 s for L₃ at each inflow velocity. This means that it takes more time for the system to reach the equilibrium of mass transfer when the length of the stagnant zone is larger. The presence of a stagnant zone induces diffusive transport processes that are slow and therefore equilibration takes longer. When the equilibration is approached, with a linear trend observed, a constant mass transfer coefficient can be obtained for the system, which is in agreement with Graveleau et al., (2017) and Maes and Soulaine (2018). The mass transfer coefficients obtained for the three cases and expressed as a dimensionless Sherwood number (according to Eq. 2) are plotted against the diffusion length (dimensionless by the characteristic length) in Fig. 6d. At each inflow velocity, it is found that the mass transfer coefficient is decreased for larger diffusion lengths, i.e., the position of the interface is at larger distances from the interface to flowing water. Comparing the Sh obtained from different inflow velocities at each diffusion length, it can be found that the mass transfer coefficient is larger for a higher water flow rate. The difference in the mass transfer coefficients at different flow rates is significantly decreased with larger diffusion lengths. The flow rate can hardly affect the mass transfer coefficient, because of the solute accumulated in the stagnant zone and the concentration profile established in the stagnant zone. This means the mass transfer process is mainly limited by the diffusive transport in the stagnant zone when the diffusion length is large (e.g., L/L_c > 1.5). Besides, for the simulations with almost no stagnant zones (at L₁), the correlation between the Sherwood number and the Reynolds number for the cavity can be formulated as:

Fig. 6

Simulation results of interphase mass transfer in a cavity: Plot of the mass transfer rates per interfacial area versus the driving force for different flow rates at stagnant zone lengths of (a) L₁, (b) L₂, and (c) L₃, where data points are collected for every 0.1 s. The crosses label the time of the beginning, the arrival of the constant slope, and the end. The dashed lines are the regression lines for the data points in the time intervals given in the legends; and (d) Sherwood number versus the dimensionless diffusion length for all simulations

$$Sh=2.62 {Re}^{0.128}$$

(24)

with R² equals 0.99.

4.2 Interphase Mass Transfer in a Porous Medium

The velocity and phase distribution patterns for pore-scale two-phase flow simulations are shown in Fig. 7. As expected, it is apparent that the domain with the larger volume of residual NAPL is obtained for lower preparation step injection rates. The phase distribution patterns obtained from the four simulations display NAPL saturations ranging from 0.236 to 0.334, as shown in Fig. 7b. At the same inflow velocity, the velocity in the channels is generally higher for higher residual NAPL saturation (see Fig. 7a, at u_in = 1 × 10^–2 m/s), because the overall space of the flowing channel in the domain is reduced. Furthermore, the process of determining the mobile and stagnant zones is identical to those described above in Sect. 4.1. The probability distributions of the local Péclet number are bimodal, as shown in Fig. 7c. The first peak on the left-hand side indicating the stagnant zone is larger at higher NAPL saturation, and the second peak on the left-hand side indicates the mobile zones. The volume of the stagnant water increases at higher NAPL saturation, and the flow pathways are more tortuous for higher NAPL saturations ranging between 0.236 and 0.334. It is obtained from the four saturation topologies: S_sw = 0.059 at S_NAPL = 0.236, S_sw = 0.103 at S_NAPL = 0.284, S_sw = 0.151 at S_NAPL = 0.298, and S_sw = 0.205 at S_NAPL = 0.334, as shown in Fig. 7. The stagnant water saturation increases with increasing NAPL saturation from S_NAPL = 0.236 to S_NAPL = 0.334. This is in agreement with Karadimitriou et al. (2017). The specific interfacial areas obtained from all simulations are close, ranging from 1240 (1/m) to 1330 (1/m). Thus, the effects of the interphase mass transfer due to the difference in the interfacial area are minimal in this study.

Fig. 7

Simulation results of two-phase flow at steady state: (a) velocity; (b) distinguished mobile and immobile zones, with the NAPL in grey color; (c) probability distribution of the local Péclet numbers, with the interval of log₁₀(Pe_l) = 0.1

The comparison of phase-averaged concentrations with time for the two examples (at u_in = 1 × 10^–4 m/s) is shown in Fig. 8a. Averaged concentrations decrease with time for both phases because solute mass transferred to the moving water is being flushed. It is also shown that phase averaged concentrations are larger for S_NAPL = 0.334 for both phases. This is mainly due to the larger initial solute mass for larger NAPL saturation. Additionally, temporal changes in the mass transfer rates are shown in Fig. 8b for the two examples. Mass transfer rates drop rapidly for the first 5 s because of the fast decrease in the driving force. The mass transfer rate is larger for S_NAPL = 0.334 after 5 s, and this is mainly due to the upkeep of the NAPL concentration maintaining a stronger driving force for higher NAPL saturation. The concentration distributions at S_NAPL = 0.236 and S_NAPL = 0.334 are shown in Fig. 8c. At a given time, the concentration is higher in NAPL clusters of larger volume, and lower interfacial area. At t = 40 s, solute concentration is depleted to a quite low value in most NAPL clusters for S_NAPL = 0.236 but still relatively high for S_NAPL = 0.334. This means that the dissolved solute remains for a relatively long time in NAPL (visible as larger retention times) for larger numbers of multi-pore, NAPL clusters. Besides, the concentration of the solute in water slightly increases in the flow direction. This is in agreement with (Hu et al., 2021). The gradient of the concentration of the solute in the water along the flow direction reduces with time.

Fig. 8

Simulation results of interphase mass transfer processes (at u_in = 1 × 10^–4 m/s) at S_NAPL = 0.236 and S_NAPL = 0.334: (a) phase-averaged solute concentration versus time; (b) mass transfer rates versus time (c) concentration distribution patterns at the time of t = 5 s and t = 40 s

From Figs. 6 and 7, it is apparent that the stagnant water phase bears higher concentrations than the mobile water phase. This means that the decrease in the driving force due to the presence of stagnant zones (discussed in Sect. 4.1) can also be observed in the porous medium. Comparing the phase distribution for S_NAPL = 0.236 and S_NAPL = 0.334 (Fig. 7), the volume of most of the stagnant water clusters is generally smaller and only one or two menisci are in contact with stagnant water clusters for S_NAPL = 0.236, while the volumes of the stagnant water clusters are larger and a larger number of menisci are in contact with stagnant water clusters for S_NAPL = 0.334. Besides, the diffusion lengths for an individual meniscus are also different according to the phase distribution for S_NAPL = 0.236 and S_NAPL = 0.334 (Fig. 7). Because each meniscus has a different length (interfacial area), and each position on the menisci can have different diffusion lengths, it is difficult to quantify the overall diffusion length of the menisci. In this case, we estimate the diffusion length for a meniscus as the shortest straight distance between the center of the meniscus and the connected flowing zone. The estimated diffusion length can be smaller than the real solute diffusion pathway length because the tortuosity of the pathway is not being considered. In Fig. 9a, an example for estimating diffusion lengths in a zoom-in region is shown for the simulation with S_NAPL = 0.334. The number of the water/NAPL interfaces exposed to stagnant zones and the average diffusion length of those interfaces in all simulations are plotted against the stagnant water saturation in Fig. 9b. It is found that both the number of interfaces exposed to stagnant zones and the average diffusion lengths of those menisci are generally larger for higher stagnant water saturation. No strictly linear increasing trend is observed because the average diffusion length also depends on the topology of the stagnant water clusters. The stagnant water saturation can generally be considered as a proxy for the overall diffusion length of the solute in the pore space starting at the menisci.

Fig. 9

Plot of (a) the estimation procedure for the diffusion length of the interfaces exposed to stagnant water clusters, in an enlarged section of the porous medium for a simulation with S_NAPL = 0.334. The interfaces, labelled 3 to 7, are exposed to the stagnant water zones, and the lengths of the dotted lines represent the estimated diffusion lengths for the individual interfaces (the white arrows show the direction of the velocity vector, and the length of the arrows is proportional to the natural logarithm of the length of velocity vector); and (b) the estimated number of interfaces exposed to the stagnant zones and the averaged diffusion length of these interfaces versus the stagnant zone saturation

Furthermore, the mass transfer rates per interfacial area are plotted versus the driving force for all simulations in Fig. 10. It is observed that the changing of the mass transfer coefficient with respect to time can be mainly separated into two stages. At Stage 1 (for the first ca. 40 s), the mass transfer rates (as the slope of the data curves) decrease continuously with time, meaning a kinetic mass transfer process. This is mainly due to the relatively faster depletion of the solute in the small NAPL clusters which are mostly in direct contact with the flowing water, as shown in Fig. 8c. Thus, the contribution of the mass transfer happened on the interface associated with small NAPL clusters (with interfaces at small diffusion length) to the overall mass transfer in the domain become less. The mass transfer happening on the interfaces at large diffusion length (mostly in large NAPL clusters) becomes dominant, and thus the overall mass transfer coefficient decreases. Though Stage 1 only lasts for about 40 s, it is shown in Fig. 8a that about 70% of the initial solute mass in the domain for S_NAPL = 0.236 and 50% for S_NAPL = 0.236 is removed from the porous domain at Stage 1. Furthermore, at Stage 2 (after the ca. 40 s), the linear trends are observed for all simulations. The linear trend is approached slightly earlier for lower NAPL saturations and lower volumes of the stagnant zones. It is observed in each subfigure of Fig. 10 that the differences in the flow rates can hardly affect the mass transfer coefficient at Stage 2. This is again because the constant mass transfer coefficients obtained at Stage 2 are mainly associated with the large NAPL clusters (with higher solute concentration remaining) with interfaces at larger diffusion lengths. This again agrees with the findings from the cavity study in Sect. 4.1. Stage 2 lasts for up to 500 s until most of the solute is removed from the porous domain.

Fig. 10

Plot of the mass transfer rate per interfacial area versus interphase concentration difference (“driving force”), with the slopes of the curves representing the mass transfer coefficients, and data points are collected for every 1 s (the crosses label the time of injection of 1.4 PVs, 2.7 PVs and 3.9 PVs of water) from simulations of (a) S_NAPL = 0.236, (b) S_NAPL = 0.284, (c) S_NAPL = 0.298, and (d) S_NAPL = 0.334. The colored dashed lines represent the regression lines at the beginning of Stage 1 (considering the first five data points), and the black dashed lines represent the regression lines at Stage 2 (for the data points in the time intervals given in the legends)

Finally, the slope of the curves at the beginning of the kinetic mass transfer at Stage 1 and the constant slope of the data curves at Stage 2 are obtained as the mass transfer coefficients, which are further expressed as Sherwood numbers (Eq. 2) and plotted against the Reynolds number and the stagnant water saturation in Fig. 11a and Fig. 11b, respectively. It is found that the Sherwood numbers obtained from the beginning of Stage1 (Fig. 11a) are strongly correlated to the Reynolds numbers (flow rates), and the effect of the stagnant water saturation on the Sherwood numbers is small. Because the overall mass transfer at the beginning is dominated by the mass transfer that happened on the interfaces in direct contact with the flowing water. The correlation function is expressed as:

Fig. 11

Plot of (a) the Sherwood numbers at the beginning of Stage 1 versus the Reynolds numbers; and (b) the constant Sherwood numbers at Stage 2 versus the stagnant water saturation. The dashed lines represent the correlation functions

$${Sh}_{1}=7.2 {Re}^{0.11}$$

(25)

On the contrary, it is found that the Sherwood numbers obtained from the Stage 2 is mainly dependent on the stagnant water saturation. For the simulations at the three flow velocities for each saturation, the obtained mass transfer coefficient is the same, as shown in Fig. 10 with the black dashed lines. The Sherwood number (mass transfer coefficient) at Stage 2 significantly decreases with larger stagnant zone saturation, as shown in Fig. 11b. The correlation between the Sherwood number and the stagnant water saturation can be expressed as:

$${Sh}_{2}=2.5 {e}^{-4.4 {S}_{sw}}$$

(26)

The obtained mass transfer coefficients range from 4.26 × 10^–6 m/s to 8.36 × 10^–6 m/s, which is smaller than the results from (Maes and Soulaine, 2018) that the mass transfer coefficient equal to 1.7 × 10^–5 m/s. The difference is mainly because their study focuses on the mass transfer process from the mobile phase into the immobile phase, where the effects of the stagnant zones are mitigated.

In this section, the NAPL distribution depends on the capillary forces in the porous medium, generated randomly and macroscopically considered homogeneous. Thus, the heterogeneity of the NAPL distribution reported as the main factor for changing the mass transfer coefficient (Agaoglu et al., 2016; Aminnaji et al., 2019), is not affected in this study. Therefore, the changes in the Sherwood number are only induced by the differences in the inflow velocity and the differences in saturation topology. The results demonstrate the importance of considering the presence and the characteristics of stagnant zones in the assessment of the interphase mass transfer coefficient.

5 Summary and Conclusions

We studied the interphase mass transfer of a dissolved species from a residual immobile NAPL phase into the flowing water phase in a domain with water-saturated flow employing the pore-scale PFM-CST model. The study was carried out in domains with geometries of a single simplified cavity and a porous medium, composed of circular grains. The flowing and stagnant zones were distinguished by applying a threshold local Péclet number. Thus, the regions of flowing water, stagnant water, and NAPL phases could be discriminated and their saturations obtained. Also, the mass transfer rates, the phase-averaged solute concentrations, and the interfacial areas were quantified. The major results and findings of the study are summarized here:

• After a period of time for the transient process at the beginning, the normalized mass transfer rate per interfacial area approaches a linearly increasing trend with increasing interphase concentration difference (“driving force”), and a constant mass transfer coefficient can be obtained for the system. This confirms that an equilibrium condition of mass transfer exists for the interphase mass transfer of a dissolved solute under given conditions.

• With the same initial solute concentration in the NAPL phase, the individual averaged concentrations in both phases are larger during the mass transfer process when the diffusion length associated with the interface is larger, and the retention time of the solute in NAPL is longer.

• For the study involving a cavity, a decrease in mass transfer coefficient is found for larger diffusion lengths (larger volumes of stagnant zones) and smaller flow velocity. When the diffusion length is small, the mass transfer coefficient can be well correlated to the inflow velocity. When the diffusion length is large (e.g., L/L_c > 1.5), the mass transfer process is mainly limited by the diffusive transport in the stagnant zone, and changes in the inflow velocity can hardly affect the mass transfer coefficient.

• For the study involving a porous medium, it is found that the number of menisci in contact with stagnant zones and the diffusion lengths of these menisci both increase with increasing stagnant zone saturations. The stagnant zone saturation can be used as a proxy for the overall diffusion length of the system.

• In the porous medium, the changing of the mass transfer coefficient can be separated into two stages. For the first stage, the mass transfer coefficient continuously decreases, due to the depletion of the solute in the small NAPL clusters that are in direct contact with the flowing water. The mass transfer coefficient at the beginning of the first stage can be well correlated to the inflow velocity. For the second stage, the mass transfer mainly happens on the interfaces associated with large NAPL clusters with larger diffusion lengths. The constant mass transfer coefficients at the second stage are determined by the stagnant zone saturation.

This study shows that the stagnant zones play an important role in the interphase mass transfer of a dissolved solute. The stagnant zone saturation is a key macro-scale parameter to be included for developing correlations with the mass transfer coefficient. Future work is required to further investigate how the mass transfer coefficient changes with respect to the factors that determine the stagnant zone saturation, such as wettability and geometry of the porous medium.

Appendix 1

The mobility (γ) from Eq. (6) is an important parameter that affects the accuracy of the results from the simulations using the PFM. The mobility is formulated as a function of the capillary thickness (ε) and a tuning factor (χ): $\gamma =\chi {\varepsilon }^{2}$, where χ is called characteristic mobility. In Appendix A, we investigate the choices of characteristic mobility and its effects on the results, by simulating a two-phase displacement process at different values of χ range from 1 to 10⁴. The simulation is implemented on a sub-region of the original geometry of porous media (Fig. 

Fig. 12

Plot of (a) the geometry of a sub-region of the original porous media and the boundary conditions for study of the choices of mobility; and (b) the region of diffusive interface with ${V}_{f,w}\in \left[0.05, 0.95\right]$ during the two-phase displacement, at different χ

12a). The boundary conditions are:$u{|}_{inlet}=0.01 m/s, p{|}_{outlet}=0,{u}_{t=0}=0, {p}_{t=0}=0$. Top and bottom boundaries are the no-flow boundaries, labelled in red lines as shown in Fig. 12a. The small section on left has ${\phi }_{t=0}=1$, the main domain has ${\phi }_{t=0}=-1$, and $\phi {|}_{inlet}=$ 1, meaning initially NAPL filled domain is drained by water. The channel wall boundary condition is no-slip. The properties of the fluids, the mesh sizes, and the capillary thickness are all the same as that explained in Sect. 3.2. The simulation results are studied by monitoring the diffusive interfacial area, as the region with ${V}_{f,w}\in \left[0.05, 0.95\right]$, which can be calculated using Eq. (22).

The diffusive interfacial area during the displacement from simulations at χ = 1, χ = 10, χ = 10², χ = 10³ and χ = 10⁴ are demonstrated in Fig. 12b. The diffusive interfacial area increases at beginning and starts to stabilized after breakthrough at about 0.06 s. The simulated fluid distribution patterns and the monitored diffusive interfacial area are similar for χ ranges from 10 to 10³, the effects of choices of χ on the results is minor within this range. It is also observed that when χ $\le$ 1, the simulated diffusive interfacial area is much larger than the results with χ $\in$[10,10³]. This is mainly due to the expansion of the interface thickness, which leads to inaccurate results. On the other hand, when χ $\ge$ 10⁴, the simulated diffusive interfacial area is much smaller than the results with χ $\in$[10,10³]. This is mainly because the flow is affected by the strong Cahn–Hilliard diffusion, and the fluid distribution pattern is changed. Thus, the suitable range of characteristic mobility is χ $\in$[10,10³] for the flow system given in Sect. 3.2.